全触分布

最近想到一个问题，发现了一个有趣的分布，姑且叫其全触分布。可能这个分布已经有了名字，不过翻了一遍概率论的书，似乎没有看到有谈过这个分布。

初始问题

假设有两台服务器，各自有独立的缓存需要预热（即初始化缓存），而预热时只能通过相同的访问地址，访问负载均衡器之后，由负载均衡器等概率随机选择一台预热，问至少需要几次地址访问，才能保证两台服务器中的缓存都被预热过的概率超过99%？

这个问题等价于一个投硬币的问题，问至少多少次伯努利试验后，才能保证正反面都出现过的概率超过99%？

令随机事件\(X\)表示，第\(n\)次伯努利试验时，才使得正反面都出现过。显然，当\(n<2\)时，事件不会发生；当\(n=2\)时，一定是一次正面一次反面；当\(n>2\)时，一定是前\(n-1\)次都是某一面，剩下的第\(n\)次是另外一面。 据此知道，随机事件\(X=n\)的概率为

$$P(X=n)=\frac{1}{2^{n-1}}$$

其中\(n \ge 2\)，而当\(n < 2\)时，\(P(X=n)=0\)。

验证所求分布律的正确性

$$P(X\ge 2)=\frac{1}{2}+\frac{1}{2^2}+…+\frac{1}{2^{n-1}}+…=1$$

分布应该如此。返回原始问题，得知在问，使得不等式\(P(X\le n)\ge0.99\)成立的最小的\(n\)为几。

由于

$$P(X\le n)=P(X=2)+P(X=3)+…+P(X=n)$$

$$=1-\frac{1}{2^{n-1}}$$

求得

$$n\ge 2\log_2{10}+1 \thickapprox7.6$$

所以，最小的\(n\)为8，即至少8次伯努利试验后才能保证正反面都出现过的概率超过99%。

问题拓展到\(m\)

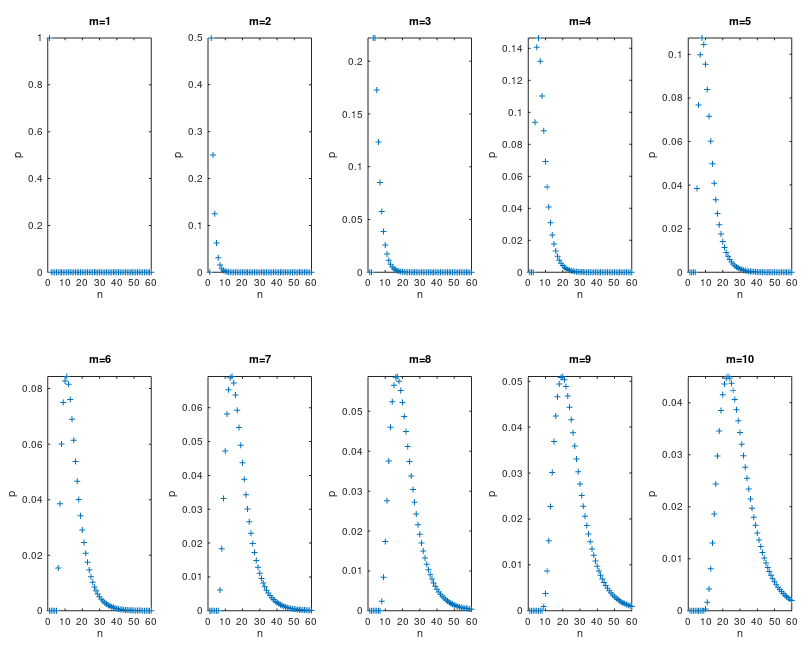
进一步，假设原始问题中不止两台机器，而是\(m\)台，伯努利试验中也不是投掷硬币，而是从\(m\)个小球中随机选，问至少多少次试验后，才能保证每台机器或者每个小球都出现过的概率超过99%？

类似地，令随机事件\(X\)表示，第\(n\)次试验时，才使得每个小球都出现过。显然，当\(n<m\)时，事件不会发生；当\(n=m\)时，一定是每个小球都只出现了一次；当\(n>m\)时，一定是前\(n-1\)次出现了\(m-1\)个小球，第\(n\)次恰好出现的是剩下的那个小球。

\(n\)次试验的概率空间容易计算，是\(m^n\)，因为每次都有\(m\)种选择，一共要选\(n\)次。对于出现随机事件\(X\)的次数，可以假设为\(F(n,m)\)次，即\(F(n,m)\)表示第\(n\)次试验时，才使得\(m\)个小球每个小球都出现过，也即

$$P(X=n|m)=\frac{F(n,m)}{m^n}$$

因为\(P(X=n|m)\)表示第\(n\)次试验时，才使得每个小球都出现过，或每个机器都被触碰过，因而称作全触分布。

最终求解的目标是\(P(X\le n | m)\ge0.99\)，而

$$P(X\le n | m)=\sum_{i=m}^{n}{P(X=i|m)}=\sum_{i=m}^{n}{\frac{F(i,m)}{m^i}}$$

所以，关键在于如何求解\(F(n,m)\)。前面分析到，当\(n>m\)时，一定是前\(n-1\)次出现了\(m-1\)个小球，第\(n\)次恰好出现的是剩下的那个小球。如果用\(G(n,m)\)表示\(n\)次试验中，\(m\)个小球都出现过的次数，那么

$$F(n,m)=m \cdot G(n-1,m-1)$$

\(G(n,m)\)不同于\(F(n,m)\)的地方在于，\(G(n,m)\)没有限制直到第\(n\)次试验，才满足\(m\)个小球都出现过，据此，有\(G(n,m)\ge F(n,m)\)。

求解\(G(n,m)\)，可以将集合划分为两个相似的缩小集合。这个划分可以根据，\(m\)个小球中的某一个是否只出现在了第\(n\)次试验中。如果某一个小球只出现在第\(n\)次试验中，那么前\(n-1\)次，就只有\(m-1\)个小球出现，即共有\(m\cdot G(n-1, m-1)\)种；如果同样的小球，不止出现在第\(n\)次试验中，那么前\(n-1\)次，仍旧有\(m\)个小球出现，共有\(m\cdot G(n-1, m)\)种。综合可得

$$G(n,m)=m\cdot G(n-1,m-1) + m\cdot G(n-1,m)$$

由以上两个等式可以知道，\(G(n,m)\)具体比\(F(n,m)\)多了多少，多了\(m\cdot G(n-1, m)\)，即

$$G(n,m)-F(n,m)= m\cdot G(n-1,m)$$

在求解\(G(n,m)\)的解析形式前，根据定义能够得出以下两个恒等式，即

当\(n<m\)时，\(G(n,m)\equiv 0\)；

当\(n=m\)时，\(G(n,m)\equiv 1\) 。

当求得解析解后，验证概率分布律时，将会再次通过代数的方式证明两个恒等式。 这是函数\(G(n,m)\)非常有趣的两个特性。

求\(G(n,m)\)的解析解

直接通过\(G(n,m)\)的递推形式，求解析形式比较困难，可以尝试用数学归纳法，先从较小的\(m\)开始。

当\(m=1\)时，\(G(n,1) \equiv 1\)。

当\(m=2\)时，\(G(n,2) = 2G(n-1,2)+2\)，解析解为\(G(n,2)=2^n-2\)。

当\(m=3\)时，\(G(n,3) = 3G(n-1,3)+3 \times (2^{n-1}-2)\)，解析解为\(G(n,3)=3^n-3\times 2^n+3\)。

当\(m=4\)时，\(G(n,4) = 4G(n-1,4)+4 \times (3^{n-1}-3\times 2^{n-1}+3)\)，解析解为\(G(n,4)=4^n-4\times 3^n + 6 \times 2^n -4\)。

如果在求解到\(m = 4\)时，还没注意到组合系数的话，那大概需要补补组合数学基础了。

有了组合系数的观察，一般地，\(G(n,m) = \sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(m-k)^n\)。

将\(m = 1, 2, 3,4\)分别依次带入方程，得出同直接由递推式求得一致的结果。

接下来验证，解析解能使递推式始终成立。由解析解方程，可知

$$G(n-1,m-1) = \sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
(m-1-k)^{n-1}$$

$$G(n-1,m) = \sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(m-k)^{n-1}$$

令第一式的\(t=k+1\)，则

\(G(n-1,m-1) = \sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
(m-1-k)^{n-1}\)
\(= \sum
_{t=1}
^{m}
{
(-1)^{t-1}
{m-1 \choose t-1}
(m-t)^{n-1}
}\)

于是

\(G(n-1,m-1) + G(n-1,m)\)

\(= \sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(m-k)^{n-1}
+
\sum
_{t=1}
^{m}
{
(-1)^{t-1}
{m-1 \choose t-1}
(m-t)^{n-1}
}
\)

\(
=
m^{n-1}
+
\sum
_{k=1}
^{m}
{
(m-k)^{n-1}
\lgroup
(-1)^k
{m \choose k}
+
(-1)^{k-1}
{m-1 \choose k-1}
\rgroup
}
\)

\(
=m^{n-1}
+
\sum
_{k=1}
^{m}
{
(-1)^k
(m – k) ^ {n-1}
\lgroup
{m \choose k}
–
{m-1 \choose k-1}
\rgroup
}
\)

\(
=m^{n-1}
+
\sum
_{k=1}
^{m}
{
(-1)^k
(m – k) ^ {n-1}
{m-1 \choose k}
}
\)

\(
=m^{n}
\cdot
\frac{1}{m}
+
\sum
_{k=1}
^{m}
{
(-1)^k
(m – k) ^ {n}
{m-1 \choose k}
\frac{m}{m-k}
\cdot
\frac{1}{m}
}
\)

\(
=
\frac{1}{m}
\cdot
\lgroup
m^{n}
+
\sum
_{k=1}
^{m}
{
(-1)^k
(m – k) ^ {n}
{m \choose k}
}
\rgroup
\)

\(
=
\frac{1}{m}
\cdot
\sum
_{k=0}
^{m}
{
(-1)^k
{m \choose k}
(m – k) ^ {n}
}
\)

所以

\(G(n,m)=m\cdot G(n-1,m-1) + m\cdot G(n-1,m)\)成立。

验证分布律的正确性

由\(G(n,m) = \sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(m-k)^n\)和\(F(n,m)=m \cdot G(n-1,m-1)\)，得知

$$F(n,m) =
m
\cdot
\sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
(m-1-k)^{n-1}$$

又\(P(X=n|m)=\frac{F(n,m)}{m^n}\)

所以

$$P(X=n|m)=
\sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
\frac
{(m-1-k)^{n-1}}
{m^{n-1}}$$

正确的分布律应满足\(P(X \ge m|m)
\equiv
1\)，即须证明

$$\sum
_{n=m}
^{\infty}
{P(X=n|m)}
\equiv
1$$

即证明

$$\sum
_{n=m}
^{\infty}
{
\sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
\frac
{(m-1-k)^{n-1}}
{m^{n-1}}
}
\equiv
1$$

即证明

$$\sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
\sum
_{n=m}
^{\infty}
{
(
1-
\frac
{1+k}
{m}
)^{n-1}
}
\equiv
1$$

即证明

$$\sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
\frac
{m}
{1+k}
(
1-
\frac
{1+k}
{m}
)^{m-1}
\equiv
1$$

即证明

$$\sum
_{k=0}
^{m-1}
(-1)^k
{m \choose 1+k}
(
1-
\frac
{1+k}
{m}
)^{m-1}
\equiv
1$$

即证明

$$\sum
_{k=0}
^{m-1}
(-1)^k
{m \choose 1+k}
(
m-1-k
)^{m-1}
\equiv
m^{m-1}$$

也即证明

$$\sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(
m-k
)^{m-1}
\equiv
0$$

观察恒等式左边，发现似曾相识，回看\(G(n,m)\)的解释式

$$G(n,m) = \sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(m-k)^n$$

发现

$$\sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(
m-k
)^{m-1}
= G(m-1, m)$$

根据前面的恒等关系

当\(n<m\)时，\(G(n,m)\equiv 0\)，得证。

等式\(\sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(
m-k
)^{m-1}
\equiv
0\)的常规证明

直接证明\(G(m-1,m)\equiv 0\)，可能没有思路，可以先从\(G(0,m)\equiv 0\)和\(G(1,m)\equiv 0\)开始。

A.?证明\(G(0,m)
=
\sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
\equiv
0\)

这个恒等式，直接用二项式展开，即可证得。根据二项式定理，知道

$$(x-1)^m
=
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
x^{m-k}$$

令\(x=1\)，即得到

$$0
=
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k$$

得证\(G(0,m)\equiv 0\)。

B. 证明\(G(1,m)
=
\sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(m-k)
\equiv
0\)

类似于A步的证明，对二项式等式

$$(x-1)^m
=
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
x^{m-k}$$

两边同时求\(x\)的导数，得

$$m\cdot
(x-1)^{m-1}
=
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
(m-k)
x^{m-k-1}$$

令\(x=1\)，即得到

$$0
=
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
(m-k)$$

得证\(G(1,m)\equiv 0\)。

C. 证明\(\sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(
m-k
)^{m-1}
\equiv
0\)

类似于B步骤的证明，对二项式等式

$$(x-1)^m
=
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
x^{m-k}$$

两边同时求\(x\)的\(n\)阶导函数（其中\(1 \le n \le m-1\)），得

$$\frac{m!}{(m-n)!}
\cdot
(x-1)
=
\sum
_{k=0}
^{m-n}
{m \choose k}
(-1)^k
\cdot
x^{m-k-n}
\cdot
\prod
_{i=0}
^{n-1}
(m-k-i)$$

令\(x=1\)，即得到

$$0
=
\sum
_{k=0}
^{m-n}
{m \choose k}
(-1)^k
\cdot
\prod
_{i=0}
^{n-1}
(m-k-i)$$

因为当\(m-n+1\le k \le m\)时，有

$$\prod
_{i=0}
^{n-1}
(m-k-i)=0$$

所以

\(0
=
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
\prod
_{i=0}
^{n-1}
(m-k-i)\)

\(=
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
\sum
_{i=1}
^{n}
a_i
\cdot
(m-k)^i\)

\(=
\sum
_{i=1}
^{n}
a_i
\cdot
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
(m-k)^i\)

因为对于所有的\(1 \le n \le m-1\)，都有

$$\sum
_{i=1}
^{n}
a_i
\cdot
\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
(m-k)^i
=0$$

因而，不论常数\(a_i\)是多少，都有

$$\sum
_{k=0}
^{m}
{m \choose k}
(-1)^k
\cdot
(m-k)^n
=0$$

成立。

得证，当\(1 \le n \le m-1\)时，

$$G(n,m)\equiv 0$$

\(\sum
_{k=0}
^{m}
(-1)^k
{m \choose k}
(
m-k
)^{m-1}
\equiv
0\)显然是\(n=m-1\)时的情况。

类似地，也能证得\(G(m,m)\equiv 1\)。

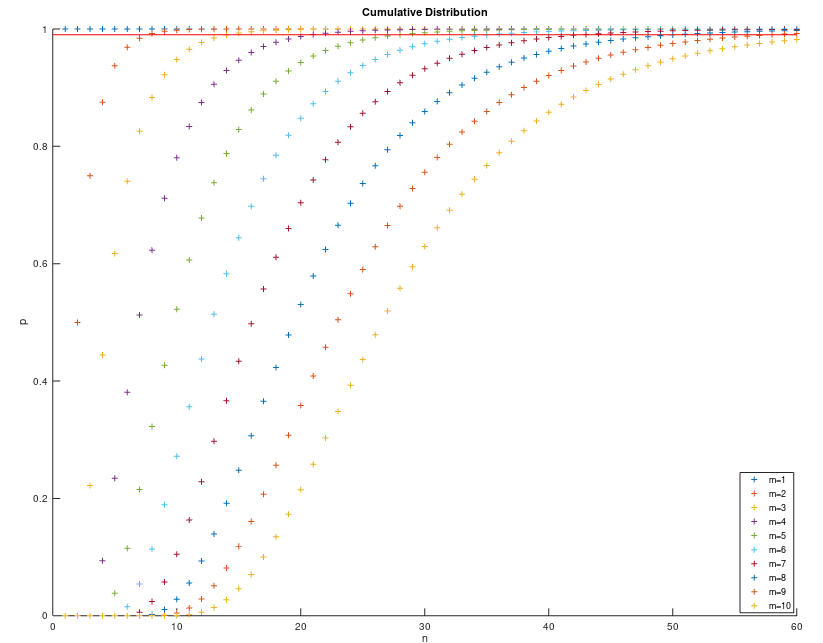
求解\(P(X\le n | m)\ge0.99\)

回到最初的目标，

\(P(X\le n | m)
=
\sum
_{i=m}
^{n}
{P(X=i|m)}\)

\(=
\sum
_{i=m}
^{n}
\sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
(1- \frac{1+k}{m})^{i-1}
\)

\(
=
\sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
\sum
_{i=m}
^{n}
(1- \frac{1+k}{m})^{i-1}
\)

\(=
\sum
_{k=0}
^{m-1}
(-1)^k
{m-1 \choose k}
\frac
{m}
{1+k}
[
(1- \frac{1+k}{m})^{m-1}
–
(1- \frac{1+k}{m})^{n}
]
\)

\(=
\sum
_{k=0}
^{m-1}
(-1)^k
{m \choose k+1}
(1- \frac{1+k}{m})^{m-1}
–
\sum
_{k=0}
^{m-1}
(-1)^k
{m \choose k+1}
(1- \frac{1+k}{m})^{n}
\)

\(
=
1
–
\sum
_{k=0}
^{m-1}
(-1)^k
{m \choose k+1}
(1- \frac{1+k}{m})^{n}
\)

若求\(P(X\le n | m)\ge0.99\)

即求

$$1
–
\sum
_{k=0}
^{m-1}
(-1)^k
{m \choose k+1}
(1- \frac{1+k}{m})^{n}
\ge
0.99$$

即求

$$\sum
_{k=0}
^{m-1}
(-1)^k
{m \choose k+1}
(1- \frac{1+k}{m})^{n}
\le
0.01$$

即求

$$0.01 \times m^n
–
\sum
_{k=0}
^{m-1}
(-1)^k
{m \choose k+1}
(m – 1 – k)^{n}
\ge
0$$

即求

$$0.01 \times m^n
–
\sum
_{k=1}
^{m}
(-1)^{k-1}
{m \choose k}
(m – k)^{n}
\ge
0$$

有此不等式，可知不同\(m\)时，满足不等式的\(n\)的最小取值，下表列举了前10项

m    1   2   3   4   5   6   7   8   9  10
n    1   8  15  21  28  36  43  51  58  66

全触分布的分布律

全触分布的累积分布函数