算术平均、几何平均和调和平均在实际生活中应用广泛,只要有度量、有统计、要比较的地方都需要它们,理解它们的差别才能更好地使用它们,不论是设计新指标还是读取报告中的指标,都要知道它指代的真实含义和局限性。
定义
- 算术平均是n个数的和除以n。
- 几何平均是n个数的积开n次方。
- 调和平均是n除以n个数的倒数和。
示例
- 算术平均:班级中有20人,20个人都参加了数学考试,拿到了20个分数,班级的平均分就是所有人的分数求和除以20。
- 算术平均:一个地区有男性人数20万,每个人都有身高,基本落在150厘米到190厘米之间,平均身高就是所有身高求和除以人数。
- 几何平均:假设股票连续四天的收益率依次是+100%、-50%、+100%、-50%,平均收益率0,也就是(1+100%)乘以(1-50%)乘以(1+100%)乘以(1-50%),然后开四次方,等于1,无收益。
- 几何平均:人口增长率连续几年下降,求这几年的平均增长率,也是相乘后开方。
- 调和平均:一艘船走同一段路程,顺流而下的速度是5米每秒,逆流而上的速度是4米每秒,平均速度是4.4米每秒。
- 调和平均:n个并联电路的电阻依次是R1, R2, …, Rn,等价于用了一个n/(1/R1+1/R2+…+1/Rn)的电阻。
动机
当我们希望用一个数字去刻画相同性质的一组数字的特征的时候,就可能需要平均数。统计学里常常需要做这样的事情,实际生活中,刻画群体特征,也需要这样的一些指标。最近看大模型中F1指标,就是Precision和Recall的调和平均,又想到了这个问题。
好处
信息从许多个压缩到了一个,比较好呈现,也容易做比较。
局限
这是一种有损的不可逆的映射,对于极端的分布,这样的指标特征刻画不够完整,也容易误导。比如一个地区的平均工资会被少数的高收入群体拉得很高。
大小
三个平均数的大小关系是
算数平均数 >= 几何平均数 >= 调和平均数
当n个数完全相同的时候,取到等号。
含义
- 不管哪种平均都意味着均匀、均等,更对称,更靠近中心的意思。
- 算术平均刻画了可叠加的多个数,分布均匀的条件下,取得同样和的那个数值是几。
- 两个数值的算术平均从几何上看,一般有两个角度。第一,当两个数值是长方形的两条边长时,有同样周长的正方形的边长就是这个算术平均数。第二,当两个数值代表两条首尾相接共线的线段时,总线段一半的长度就是算数平均数。
- 算数平均到三维的几何含义,第一个角度可以说立方体的表面积,第二个角度可以说质心的坐标位置,更高维依然可以这样类比。第一个角度叫做和等效均衡,第二个角度是线性均衡,或者说空间中心趋势。
- 几何平均刻画了可叠乘的变量,分布均匀的条件下,取得同样积的那个数值是几。
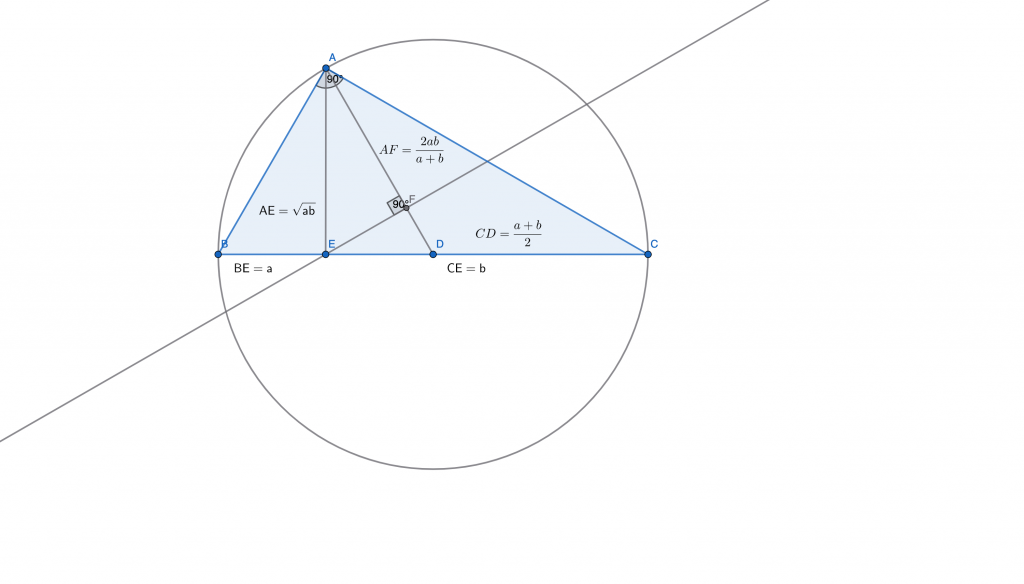
- 两个数值的几何平均从几何上看,一般也有两个角度。第一,当两个数值代表长方形的两条边长时,得到同样面积的正方形的边长就是这个几何平均数。第二,当两个数值代表两条首尾相接共线的线段时,以总线段中点为圆心,总线段一半长为半径做圆,从相接点向圆做垂线,这段垂线段长度就是几何平均数。
- 几何平均到三维的几何含义,第一个角度可以说得到相同体积的立方体边长,是积等效均衡,第二个角度可以说三个数的比例均衡。
- 调和平均刻画了完成同样一件事情不同方法或者不同角度的效率的平均。
- 调和平均的几何意义是面积相同的n个长方形,若各自的底长度不变,得到总面积不变的一个大的长方形的高也就是原来n个高的调和平均。
用途
- 可叠加的量求平均用算数平均,比如路程、时间、人数、分数、身高、体重、长度等等。
- 增长率一类叠乘的量求平均用几何平均,比如经济增长率、投资收益率、人口增长率、声音频率等等。
- 效率一类倒数可叠加的量求平均用调和平均,比如速度、折射率、电阻并联等等。
讨论
三个平均数在很多时候,从计算的数值上看,差别并不大,似乎不用那么严格影响也不大。比如一个人90分,一个人80分,算数平均是85.00分,几何平均是84.85分,调和平均是84.71分,用哪个也都差不过一分。但一些特殊情况就不那么回事了,比如一个人10分,一个人90分,这个差别就大了,如果有一个0分,几何和调和就都得0分了,或者严格来说调和无意义,0不能取倒数。再比如前面举的收益率的例子,如果用了算数平均就会错误地判断四年的平均增长率是+25%,但实际上四年的平均增长率是零。因此,实际应用中,一定要注意量的实际含义,选择合适的平均数。
